Distance,Velocity-Time Graphs
Home Return

Page Contents
Distance-Time graph  
Velocity-Time graph  

Distance-time Graph

  1. What is a distance-time graph?
         A distance-time graph simply shows the relationship between time and position.
    For example, given the following data,  plot the position-time graph? We can draw the following graphs.
    Data

    time (s)

    		 position (s)
    0 0
    1 20
    2 50
    3 130
    4 150
    5 200
  2. How do we evaluate the average velocity between two points? 
         The tangent of a distance-time graph represents velocity since
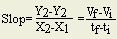  3. From the given curve,  what is the average velocity during the first 2 seconds?
  4. From the given curve,  what is the average velocity of the whole trip?
 

Velocity-time Graph

  1. What is velocity-time graph?
    A velocity-time graph shows the relationship between velocity and time. 
  2. If a car moves at constant velocity of 5 m/s for 10 seconds. Plot a velocity-time graph. 
    Data

    time (s)

    		 Velocity (s)
    0 20
    1 21
    2 24
    3 27
    4 28
    5 30

     
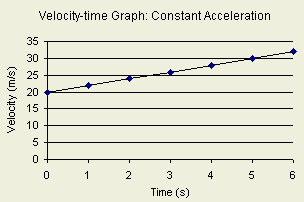  3. What are the types of data that we can obtain from a velocity-time graph?
         1- Instantaneous velocity at any time
         1- Directly from velocity axis at the edges of segments.
         2- Within none linear segments approximate v to be within v2 and v1.
         3- Within linear segments use v=s(t-t1)+v1, s=(v2-v1)/(t2-t1)
          
         
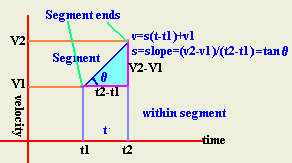
    2- Acceleration at any time "t".
         Acceleration=Segment Slope
    3- Average Acceleration at any time interval (ti,tf)
         a=Vf-Vi/(tf-ti)
    4- Traveled Distance at any time interval (ti,tf)
         Traveled Displacement=Area Under the curve between ti and tf.
         The area below the line represents the displacement the object traveled since it can
         be calculated by (time * velocity) which equals to displacement.
    5    - Average-velocity at any time interval (ti,tf)
         Average-velocity=Traveled Distance/(tf-ti)
  4. What is the significance of the area under the velocity-time curve 
          The area below the line represents the displacement the object traveled since it can
         be calculated by (time * velocity) which equals to displacement.
  5. What is the significance of tangent of a velocity-time graph?
     the tangent of a velocity-time graph represents instantaneous acceleration since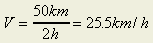
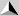
     For example, the instantaneous acceleration when t = 3 at the below graph is 3 m/s2, since the graph has a slope of 3 when t = 3.
  6. What is the instantaneous acceleration of the above object when t = 0?
  7. What is the average acceleration of the whole trip? (When t = 7, velocity = 26 m/s)
  8. Does above object has a constant acceleration?
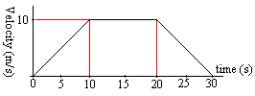
  9. From the velocity-time graph shown.  Find the followings

    1.  Acceleration within the first 5 seconds

    2. Acceleration at t=15 seconds

    3.   Distance traveled within the first 20 seconds

    4.  Average speed within the last 10 seconds

     

     

For more information write: abumsamh@emirates.net.ae
Created SEP 1, 2000
Copyright © 2000
Designed by: R. K. Abu-Msameh
Last modified: May 29, 2001