|
Projectile Motion
Objects launched are called projectiles. The flight of baseballs and
basketballs are some examples of projectile motions.
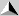 Dropping a Ball Dropping a Ball
- Draw a free diagram of a free fallen object
- Why when we drop a ball, the velocity in the
horizontal-direction is zero?
Since we did not applied no
force on x-direction, the velocity on x-direction is zero and the
acceleration is also zero.
- Why when we drop a ball, it accelerates with 9.8
m/s2.?
The ball will fall because of gravity. We know that the force of
gravity applies to any object. The ball's acceleration on y direction is
-9.8 m/s2. Its initial velocity is zero.
- Why the velocity of the ball does not depend on
mass?
The velocity of the ball is not dependent on its mass.
- What are the factors which the velocity of the
ball depend on?
The velocity is dependent on its surface area and air resistance.
- Explain how do we calculate position, velocity, and
acceleration of a falling ball at a given time t.
| |
Displacement |
Velocity |
Acceleration |
| x-direction |
d = 0 |
v = 0 |
a = 0 |
| y-direction |
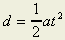 |
v = at |
a = -9.8 |
In this type of projectile, an object is throwing in horizontal direction with an
initial velocity of A. This velocity will stay unchanged since there is no force that will
influence its movement in horizontal direction. The acceleration on x
direction is zero, because the net force on the ball is zero.
Also, the ball accelerate downward with -9.8m/s2 because gravity is the only force acting on it, the ball will accelerate at the
rate of -9.8 m/s2
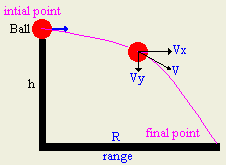
The following table shows how to calculate displacement, velocity,
and acceleration of the ball.
| |
Displacement |
Velocity |
Acceleration |
| x-direction |
dx = At |
Vx = A |
a = 0 |
| y-direction |
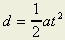 |
Vy = at |
a = -9.8 |
| motion |
d=(dx2+dy2)½
q=tandy/dx |
V=(Vx2+Vy2)½
q=tanVy/Vx |
|
- When the object reaches ground?
When the displacement in the
y-direction is zero.
- How long will it take the ball to reach
the ground surface?
t=(2h/g)½
- What is the range of the ball in the
horizontal direction?
x=A(2h/g)½
In this type of projectile a ball is through with angle with respect to the
horizontal direction with an initial velocity V0.
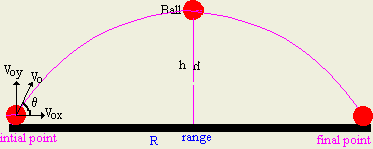
We can break down V0 into V0x and V0y
The velocity on x direction is Vx. The acceleration on x is zero.
The velocity on y direction is Vy. The acceleration on y is -9.8
m/s2.
| |
Initial Velocity |
Displacement |
Velocity |
Acceleration |
| x-direction |
V0x = V0 cosq |
dx = V0x * t |
Vx = V0x |
a = 0 |
| y-direction |
V0y = V0 sinq |
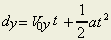 |
Vy = V0y + at |
a = -9.8 |
| motion |
V0 |
d=(dx2+dy2)½
q=tandy/dx |
V=(Vx2+Vy2)½
q=tanVy/Vx |
|
- When the object reaches ground?
When the displacement in the
y-direction is zero.
- When the object reaches the highest
point in the vertical direction?
When its velocity in the
y-direction is zero
- What is the range of the ball in the
horizontal direction?
- How long will it take the ball to reach
the ground surface?
- What is the maximum height ball can
reach?
- At what angle the range of a ball can be
maximum?
When you throw a ball on a rug, it doesn't bounce much. When you
throw the ball to floor, it bounces higher. The reason is in the
coefficient of bounce.
Whenever two objects collide, the following equation is true:
V2 = e * V1
where V1 is the velocity before collision, V2
is the velocity after collision, and e is a constant. This constant e is
called the coefficient of bounce, which ranges from 0 to 1. When there
is no friction between the two objects, e = 1. As the friction
increases, the value of e approaches to 0.
We can say that a rug has a lower coefficient of bounce than floor.
Probably e = 0.2 in a rug, and e = 0.8 on floor.
 Test
Yourself Test
Yourself
| 