|
 Distance-time Graph
Distance-time Graph
- What is a distance-time graph?
A distance-time graph simply
shows the relationship between time and position.
For example, given
the following data, plot the position-time graph? We can draw the
following graphs.
| Data |
|
time
(s)
|
position (s) |
| 0 |
0 |
| 1 |
20 |
| 2 |
50 |
| 3 |
130 |
| 4 |
150 |
| 5 |
200 |
|
 |
How do we evaluate the average velocity between two
points?
The tangent of a distance-time graph represents velocity since
 From the given curve, what
is the average velocity during the first 2 seconds?
From the given curve, what
is the average velocity of the whole trip?
Using the following distance-time graph
describe the motion.
From the given curve, what
is the average velocity during the first 2 seconds?
From the given curve, what
is the average velocity of the whole trip?
Using the following distance-time graph
describe the motion.
| No |
Segment Description |
Distance |
Velocity |
Acceleration |
| 1 |
Linear, +slope |
increasing |
constant |
zero |
| 2 |
Curved-up |
increasing |
increasing |
increasing |
| 3 |
curved-down |
increasing |
decreasing |
decreasing |
| 4 |
straight-line |
constant |
zero |
zero |
| 5 |
curved-down |
decreasing |
increasing |
increasing |
| 6 |
curved-up |
decreasing |
increasing |
increasing |
| 7 |
linear, -slope |
decreasing |
constant |
zero |
| 8 |
linear, -slope |
increasing |
constant |
zero |
| 9 |
curved-down |
increasing |
not constant |
increasing |
| 10 |
curved-up |
increasing |
decreasing |
decreasing |
| 11 |
straight-line |
constant |
zero |
zero |
| 12 |
curved-down |
decreasing |
increasing |
increasing |
| 13 |
curved-up |
decreasing |
increasing |
increasing |
| 14 |
linear, +slope |
decreasing |
constant |
zero |
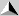
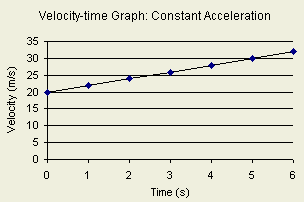
 Velocity-time Graph Velocity-time Graph
- What is velocity-time graph?
A velocity-time graph shows
the relationship between velocity and time.
- If a car moves at constant velocity of 5 m/s for
10 seconds. Plot a velocity-time graph.
| Data |
|
time
(s)
|
Velocity (s) |
| 0 |
20 |
| 1 |
21 |
| 2 |
24 |
| 3 |
27 |
| 4 |
28 |
| 5 |
30 |
|
 |
What are the types of data that we can obtain from a
velocity-time graph?
1- Instantaneous velocity at any time
Directly from velocity axis
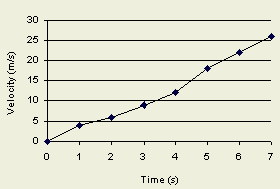
2- Average Acceleration at any time interval (ti,tf)
a=Vf-Vi/(tf-ti)
3- Traveled Distance at any time interval (ti,tf)
Traveled Distance=Area Under
the curve between ti and tf.
The area below the line represents the displacement
the object traveled since it can
be calculated by (time * velocity) which equals to
displacement.
4- Average-velocity at any time interval (ti,tf)
Average-velocity=Traveled
Distance/(tf-ti)
What is the significance of the area under the velocity-time curve
The area below the line
represents the displacement the object traveled since it can
be calculated by (time * velocity) which equals to
displacement.
What is the significance of tangent of a velocity-time graph?
the tangent of a velocity-time graph represents
instantaneous acceleration since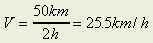
For example, the instantaneous acceleration when t = 3 at the below graph
is 3 m/s2, since the graph has a slope of 3 when t = 3.
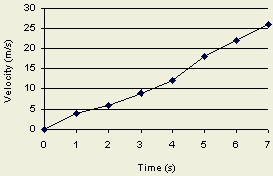 What is the instantaneous
acceleration of the above object when t = 0?
What is the instantaneous
acceleration of the above object when t = 0?
What is the average
acceleration of the whole trip? (When t = 7, velocity = 26 m/s)
Does above object has a
constant acceleration?
Using the following distance-time graph
describe the motion.
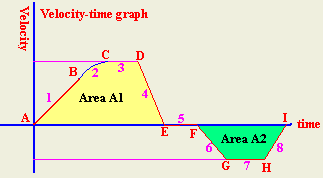
| No |
path |
Segment Description |
Velocity |
Acceleration |
| 1 |
AB |
Linear, +slope |
increasing |
constant |
| 2 |
BC |
Curved-down |
increasing |
decreasing |
| 3 |
CD |
straight |
constant |
zero |
| 4 |
DE |
Linear, - slope |
decreasing |
constant deceleration |
| 5 |
EF |
straight |
stationary |
zero |
| 6 |
FG |
Linear, - slope |
decreasing |
constant |
| 7 |
GH |
straight |
constant |
zero |
| 8 |
HI |
linear, +slope |
increasing |
decreasing |
| |
Distance=A1+A2
Displacment=A1-A2 |
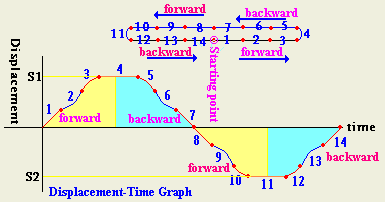
Using the following distance-time graph
describe the motion.
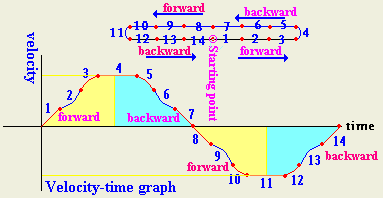
| No |
Segment Description |
Velocity |
Acceleration |
| 1 |
Linear, +slope |
increasing |
constant |
| 2 |
Curved-up |
increasing |
increasing |
| 3 |
curved-down |
increasing |
decreasing |
| 4 |
straight-line |
constant |
zero |
| 5 |
curved-down |
decreasing |
decreasing |
| 6 |
curved-up |
decreasing |
decreasing |
| 7 |
linear, -slope |
decreasing |
constant |
| 8 |
linear, -slope |
increasing |
increasing |
| 9 |
curved-down |
increasing |
increasing |
| 10 |
curved-up |
increasing |
increasing |
| 11 |
straight-line |
constant |
zero |
| 12 |
curved-up |
increasing |
increasing |
| 13 |
curved-down |
increasing |
increasing |
| 14 |
linear, +slope |
constant |
constant |
| |
Distance=A1+A2
Displacment=A1-A2 |
|
|

|



