 | Scalar quantities, vector quantities |
 | Addition and subtraction of two vectors |
 | Vector components |
 | Addition and subtraction of more than two vectors |
Scalars and Vectors
- What is meant by a scalar quantity? Give examples?
A scalar quantity has only magnitude. Distance,
speed, mass, energy, volume, charge ..etc.
- What is meant by a vector quantity? Give examples?
A vector quantity has both magnitude and
direction. displacement, velocity, force, weight,
acceleration, momentum, torque
- How do we express vectors in writing and in
graphing?
In writing we use bold type (e.g. A) or
by placing an arrow above the symbol (e.g. A).
In graphics, they are drawn in lines with arrows. The arrow
represents the direction and the line length represents the vector
magnitude.
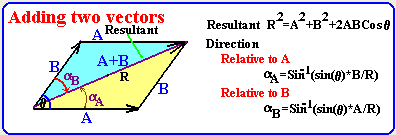
- How do we add two vectors A, B?
The figure shown below shows two vectors A
and B with angle "q" of between
them. The two vectors are pointing out of their joint point. The
result of adding these vector is a vector is referred to by R where R=A+B.
The magnitude of the R vector is given by the formula shown and the
directions are given relative to the A and B vectors.
- Find the magnitude of the resultant of a 20 N force
acting at 60 to 30N force and direction relative to the 20N and 30N forces.
1- We first draw the forces and complete the
four sides of to form a parallelogram as shown in figure below.
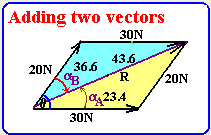
2- Let A=20N and B=30N and substitute in the formula R2=A2+B2+2ABCos(q)=202+302+2
20 30 1/2 Cos(60)=400+900+600=1900. Thus, R=1900(1/2)=43.6
N
3- We substitute in direction formula relative to 20N force
aA=sin-1(B* sin(q)/R)= sin-1(30*sin(60)/43.6)=36.6
3- We substitute in direction formula relative to 30N force
aB=sin-1(A
* sin(q)/R)= sin-1(20*sin(60)/43.6)=23.4
- How do we subtract two vectors A, B?
The figure shown below shows two vectors A
and B with angle "q" of between
them. The two vectors are pointing out of their joint point. The
result of subtracting these vector is a vector is referred to by R
where R=A-B. The magnitude of the R vector is given by
the formula shown and directions are given relative to the A and B
vectors.
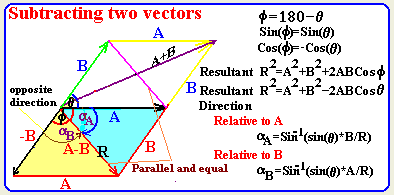
We subtract vectors by adding them. Assume A and B are the
original vectors. The '-B' vector lies on the same line of the 'B'
but on opposite directions as shown. Now, we have the 'A' and '-B'
vectors pointing outward their joint point with an angle of "f"
where f+q=180. By applying the formula of vector
addition we obtain R=A+ (-B) where R2=A2+B2+2ABCos(f).
But since f+q=180 we have Cos(f)=-Cos(q)
and hence we get R2=A2+B2-2ABCos(q).
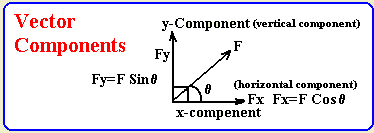
- How do we find the components of a vector?
1- We determine the angle between the vector
and one of its components
2- The components that makes the angle with the vector takes the cosine
3- The components that does not make the angle with the vector takes the
sine
4- Both components are perpendicular
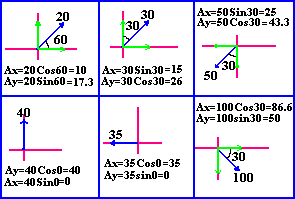
- Find the x-components and y-components of all forces
shown below.
Solution is provided on same graph.
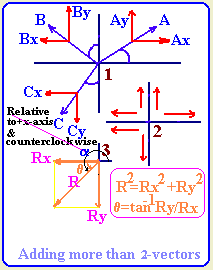
- How do we add more than two vectors?
1- We break each vector into its components
2- We add all x-components and refer to it as Rx
3- We add all y-components and refer to it as Ry
4- We find the resultant R from Rx and Ry using R2=(Rx2+Ry2)½ since Rx and Ry are
perpendicular
5- We find the direction angle relative to Rx by
q=tan-1(Ry/Rx).
6- Convert
q to be relative to +x-axis and
moving counter clockwise to the resultant.
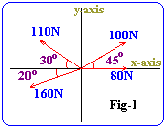
- Find the resultant of the system of forces shown
below.
| No |
Force |
Angle |
X-comp |
y-comp |
| 1 |
80 |
0 |
80cos0= 80 |
80sin0= 0 |
| 2 |
100 |
45 |
100cosa45 =71 |
100sin45= 71 |
| 3 |
110 |
30 |
-110cos30= -95 |
110sin30= 55 |
| 4 |
160 |
20 |
-160cos20= -150 |
160sin20= -55 |
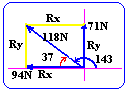
| |
|
|
Rx=-94 |
Ry=71 |
R=(Rx2+Ry2)½=(942+712)½=118N
q=tan-1 Ry/Rx=tan-171/94=37
a=180-q=180-37=143
see graphs to right |
|
 |
|