Information
- What is meant by Coplanar forces?
Coplanar forces are forces whose line of action
never intersects.
- What is the physical meaning of torque (moment)?
Torque is a measure of the effectiveness of a
force in producing rotation about an axis.
- What is the definition of torque?
Torque is defined to be the product of the
force and the perpendicular distance from the axis of rotation to the line
of action of the force. Mathematically, torque=(force)(lever-arm), symbolically,
t= f*d
- What is meant by level-arm or moment arm?
It is the perpendicular distance from the axis
of rotation to the line of action of the force.
- What are the equilibrium conditions under coplanar
forces?
1) SF=0 :1-
SFx=0 2- SFy=0
3- SFz=0
2) (St)A=0
- States the principle of moments?
The sum of moments at any point in the system
is zero. (St)A=0
- What are the directions of torque?
A torque that tends to cause a clockwise
rotation is negative
A torque that tends to cause a counterclockwise rotation is positive
- What is meant by Center of Gravity?
Is the point at which the entire weight of the
object may be considered concentrated.
- How to solve coplanar equilibrium problems:
1- Draw a free body diagram
2- Replace weights by an equivalent force at the center mass
3- Show reaction forces at joints
4- Apply force conditions SF=0 :1-
SFx=0 2- SFy=0
3- SFz=0
5- Apply torque condition (St)A=0at a
point with the maximum number of unknown forces.
-
Problems
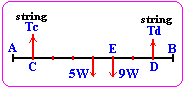
- A uniform pole AB of weight 5W and length 8a is
suspended horizontally by two vertical strings attached to it at C and D where
AC=DB=a. A body of weight 9W hangs from the pole at E where ED=2a.
Calculate the tension in each string. (problem 6/49)
1-
SFy=0: Tc+Td-9W-5W=0
2- (St)d=0:
Tc6a-9W2a-5w3a=0
Tc=33W/6=5.5W
Td=9W+5W-Td=14W-5.5W=8.5W |
 |
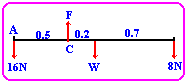
AB is a uniform rod of length 1.4m. It is pivoted at
C, where AC=0.5m, and resets in horizontal equilibrium when weights of 16N and
8N are applied at A and B respectively. Calculate: (a) the weight
of the rod, (b) the magnitude of the reaction at the pivot. (problem-7/49).
1-
SFy=0: -16+F-W-8=0
2- (St)c=0:
16*0.5-w*0.2-8*9=0
W=(8-0.2W-7.2) /0.2=0.8/0.2=4N
F=16+4+8=28N |
 |
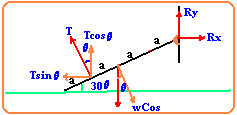
A uniform rod AB of length 4a and weight W is
smoothly hinged at its upper end, A. The rod is held at 30 degrees to
the horizontal by a string which is at 90 degrees to the rod and attached to
it at C where AC=3a. Find (a) the tension in the string, (b) the
vertical component of the reaction force, (c) the horizontal component of the
reaction at A. (problem-9/49)
1-
(St)A=0: T
2a-2a*WCos30=0
T=(2/3)WCos30=0.58N
2-
SFy=0: Ry+Tcos30-w=0
Ry=W-TCos30=W(1-0.58Cos30)=0.5W
Rx=Tsin30=0.5WSin30=0.29W
|
 |
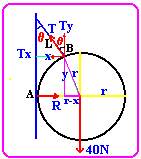
A sphere of weight 40N and radius 30cm rests against
a smooth vertical wall. The sphere is supported in this position by a
string of length 20cm attached to a point on the sphere and to a point on the
wall. Find: (1) the tension in the string, (b) the reaction due to the
wall. (problem-9/49).
1- SFy=0: TCosq=W
2- SFx=0: TSinq=R
from (1) & (2) T2=R2+W2
(Stx)A=0:
yTsinq+xTCosq=Wr
(Stx)B=0:
Ry=w(r-x); x=LSinq
From the above equations we can derive the following relation
of "q". as Sinq=r/(r+L)
where "L" is string length and "r" is sphere radius.
From which we obtain sinq=30/(30+20)=3/5, q=36.9.
T=w/Cosq=40/Cos36.9=50N,
R=w tanq=40tan36.9=30.
Bonus: show that Sinq=r/(r+L)
and get five points on your exam |
 |
end
|