-
 |
Concurrent
forces, weight, tension, friction |
 |
Equilibrium
Conditions |
 |
Problem Solution |
 |
Kinetic friction, Static friction, coefficients and laws of friction |
Information
- Define the following terms?
 | Concurrent forces: Are forces whose lines of action all pass through a
common point. |
 | Weight: is the force with which the gravity pulls downward upon it. |
 | Tension in string: is the force with which the strings pulls upon the
object to which it is attached. |
 | Friction force: is a tangential force on a surface that opposes the
sliding of a surface across an adjacent surface. |
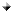 | Normal force: is the perpendicular component of the force exerted by
the supporting surface on the surface being supported. |
What are the equilibrium conditions under the action of concurrent forces?
The resultant of all forces acting on an object
must be zero. or
1- The sum of all x-components is zero.
2- The sum of all y-components is zero.
3- The sum of all z-components is zero.
When an object is in equilibrium
If it is at rest and remains at rest. or if it
is in motion with constant vector velocity
What are the types of equilibrium
Static-Equilibrium: The object it is at rest
and remains at rest.
Translational-Equilibrium: The object is in motion with constant vector
velocity
How do you solve problems in equilibrium under
concurrent forces?
1- Isolate the object under forces
2- Draw a free-body diagram
3- Find all the x,y,z-components of each force in the system
4- Write the conditions for equilibrium in an equation form
5- Solve for the unknowns from the equations obtained in step-4.
Problems
- The system shown below is in equilibrium. Solve for T1 and T2.
1- SFx=0,
-T1Sin30+T2Sin60=0, -0.5T1+0.866T2=0
T1=1.73T2
2- SFy=0, T1Cos30+T2Cos60-20=0,
0.866T1+0.5T2=20
From (1) 0.866(1.73T2)+0.5T2=20, 1.50T2+0.5T2=20
T2=20/2=10 N
T1=1.73T2=17.3 N |
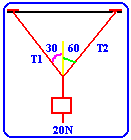 |
Two forces, P and Q, act NW and NE respectively. They are in
equilibrium with a force of 50.0 N acting due E. Find P and Q.
1- SFx=0,
QSin45+20-PSin45=0
0.7Q-0.7P=-20
2- SFy=0,
QCos45+PCos45-50=0
0.7Q+0.7P=50
By adding (1) & (2) 1.4Q=30, Q=30/1.4=21.4 N
From (1) P=(Q+20/0.7)=49.9N |
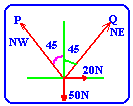 |
A particle whose weight is 50N is suspended by alight string which is at
35 degrees to the vertical under the action of a horizontal force F.
Find: (a) the tension in the string, (b) F.
1-
SFx=0, F-TSin35=0
2- SFy=0, TCos35-50=0
From (2) T=50/Cos35=61N
From (1) F=TSin35=61Sin35=35 N |
 |
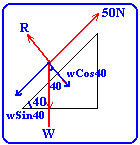
A particle of weight W rests on a smooth plane which is inclined at 40
degrees to the horizontal. The particle is prevented from slipping by
a force of 50N acting parallel to the plane and up a line of greatest
slope. Calculate (a) W, (b) the reaction due to the plane.
1- SFx=0,
50-wSin40=0
W=50/Sin40=77.8 N
2- SFy=0, R-wCos40=0
R=wCos40=59.6 N
|
 |
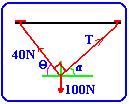
Two light strings are perpendicular to each other and support a particle
of weight 100N. The tension in one of the strings is 40N.
Calculate the angle this string makes with the vertical and the tension in
the other string.
1- SFx=0,
TCosa-40Cosq=0
2- SFy=0, 40Sinq+TSina-100=0
Since q+a=90,
we have
Sinq=Cosa
and
Cosq=Sina
1- TSinq-40Cosq=0
2- TCosq+40Sinq=100
Multiply (1) by
Cosq
and (2) by
Sinq.
1- -TCosqSinq+40CosqCosq=0
2- TSinqCosq+40SinqSinq=100Sinq
40(Sin2q+Cos2q)=100Sinq,
Sinq=0.4, q=23.5,
a=90-q=90-23.5=66.4
|
Notes:
1) When q+a=90, then
Sinq=Cosa
Cosq=Sina
2)Sin2q+Cos2q=1
|
|