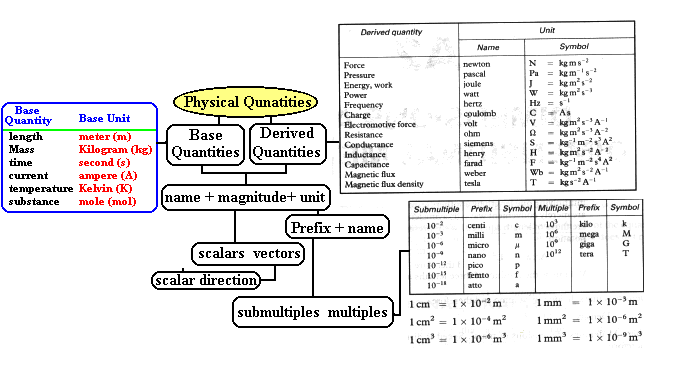
Quantities, Units, SI units
	Base Quantities, Base units
	Derived quantities, Derived units
	Homogenous, Correct/incorrect equations
	Prefixes

1. What is meant by a physical quantity?
   A physical quantity is a measure to a physical parameter.
2. What are the two major components of physical quantity?
   1- Magnitude  2- Unit
3. What does "SI" means?
   It means International System of Units.
4. What are the Base ( Basic) Quantities?
   length, mass, time, current, temperature, amount of substance
5. What are the basic units in SI system?
   Kilogram (Kg), meter (m), second (s), ampere (A), Kelvin (K), mole (mol)
   candela (cd)
6. List the main definition of the Base units.

   Unit	Abbv.	Definition
   metre (meter)	m	The metre is 1 650 763.73 of the wavelength, in vacuo of the orange light emitted by 86Kr in the transition 2p10 to 5d5.
   kilogram	kg	The kilogram is defined as the mass of a platinum-iridium cylinder kept at Sevres, near Paris. This definition is not recommended for work of high precision.
   second	s	The time taken by 9 192 631 770 cycles of radiation from the hyperfine transition in caesium when unperturbed by external fields.
   ampere	A	That constant current which, if maintained in each of two infinitely long straight parallel wires of negligible cross-section placed 1 metre apart in a vacuum, will produce between the wires a force of 2 x 10-7 newtons per metre length.
   mole	mol	The amount of substance which contains as many elementary entities as there are atoms in 0.012 kilogram of the carbon isotope 12C.
   kelvin	K	The kelvin is the fraction 1/273.16 of the thermodynamic temperature of the triple point of water.
   candela	cd	The luminous intensity, in the perpendicular direction, of a surface of 1/600 000 square metre of a full radiator at the temperature of freezing platinum under a pressure of 101 325 newtons per square metre.

7. What is meant by a derived unit, give an example?
   Any unit not listed in based unit is called a derived unit. A derived unit is usually formed by multiplying or/and dividing the Basic-Units.  Example: Force=mass*acceleration,  Newton=kilogram*  m/sec². The following table lists derived quantities and units.  The table also shows the formula from which the unit was derived.

   No	Derived Quantity	Formula	Unit Name	Unit Symbol
   1	Force	F=ma	newton	N=Kg m s-1
   2	Pressure	p=F/A	pascal	Pa=Kg m-1s-1
   3	Energy, work	W=Fd	joule	J=Kg m2s-2
   4	Power	P=dw/dt	watt	W=Kg m2s-3
   5	Frequency	---------	Hertz	Hz= s-1
   6	Charge	q=It	Columb	C=As
   7	Electromotive force	P=VI	volts	V=Kg m2s-3A-1
   8	Resistance	V=IR	Ohm	W=Kg m2s-3A-2
   9	Conductance	G=1/R	siemens	S=Kg-1 m-2s3A2
   10	Inductance	e=Ldi/dt	henry	H=Kg m2s-2A-2
   11	Capacitance	C=Q/V	farad	F=Kg-1 m-2s4A2
   12	Magnetic flux	F=nEt	weber	wb=Kg m2s-2A-1
   13	Magnetic flux density	B=F/A	tesla	T=Kg s-2A-1

8. How do we simplify complex derived units. give examples?
   By naming them.  Ohm=Kg m² s^-3 A^-2
9. What is meant by a homogenous equation?  Give an example?
   A homogenous equation is an equation where the units of  its right side are equal to the units of that of its left side.
   F=m a, [N]=[m][a],  kg m s^-2=kg m s^-2.  All units on the two sides are equal
10. When do we refer to an equation as a correct equation? Give example.
    When both sides of an equation give the same units, same numerical values, and same concept we refer to the equation as being correct. The area of a sphere is A=4pr³.  This equation is correct because its sides give the same results.
11. How do we give a homogenous equation but an incorrect equation at the same time?
    1. Removing constants from correct equations make them homogeneous but incorrect.  For example, the correct formula for kinetic energy is K.E.=(1/2) m v².  If we remove the constant 1/2 we get K.E=m v², which is homogenous but incorrect.
    2. Adding constants to correct equations make them homogeneous but incorrect.  For example, the correct formula for pressure p=F/A.  If we add a constant say "2" we get p=2F/A, which is homogenous but incorrect.
    3. Mixing concepts with similar units. For example, work, Kinetic energy, and potential energy have the same units but saying the potential energy is P.E=(1/2)mv2 is incorrect.
    4. Mixing equations with similar terms. For example, work is defined as W=F*D and torque is defined as G=F_^*D. So, the equation w=F_^*D is homogenous but incorrect.
12. What is meant by a unit-prefix? Give an example?
    A prefix is used with unit symbols to indicate decimal multiples or submultiples.
    kilogram (prifix=kilo and unit is gram)
    
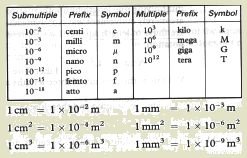13. What are the common multiple-prefixes?
    Kilo (k)=10³, mega (M)=10⁶, giga (G)=10⁹, tera (T)=10¹²
14. What are the common submultiples-prefixes? Give examples
    centi (c)=10^-2, milli (m)=10^-3, micro (µ)=10^-6, nano (n)=10^-9, pico (p)=10^-12, femto (f)=10^-15, atto (a)=10^-18
    Kilogram, nanosecond, 10 Mega bytes,  1 Giga Byte, 5 cm,

1. With the aid of an example, explain the statement "The magnitude of a physical quantity is written as the product of a number and a unit"
2. Explain why an equation must be homogeneous with respect to the units if it is to be correct?
3. Write down an equation which is homogeneous , but still incorrect?
4. Kepler discovered that the period T of the planets about the Sun are related to their distances "r" from the Sun.  From Newton's laws, the following equations may be derived T²=(4p²/GM)r³.  Use the equation to find the units for the G in terms of base units.
5. For each of the four concepts listed in the left hand column, place a tick by the correct example of that concept in the appropriate box.
   

   Concept	Example	Example	Example
   Base unit	c mole	c length	c Kilograms
   Derived unit	c coulomb	c ampere	c volt
   Base Quantity	c torque	c velocity	c kinetic energy
   Derived Quantity	c mass	c density	c density

6. Demonstrate that the following equation is homogeneous with respect to units.  The symbols have their usual meanings.  x=ut+(1/2)a t².
7. Classify each of the units in the left-hand column by placing a tick in the relevant box.

   	Base unit	Derived unit	Base quantity	Derived quantity
   Length	c	c	c	c
   Kilogram	c	c	c	c
   Current	c	c	c	c
   Power	c	c	c	c
   Coulomb	c	c	c	c
   Joule	c	c	c	c

8. Each row in the following table starts with a term in the left hand column.  Indicate with a tick which of the three expressions in the same raw relates to the first term.

   Joule	kg.m.s-2 c	kg.m2.s-2 c	kg.m2.s-3 c
   Coulomb	Base unit c	derived unit c	Base quantityc
   Time	Scalar Quantity c	Vector Quantity c	neither vector nor scalarc
   volt	AxW c	AxW-1 c	WxA-1 c

9. Each row in the following table contains two correct statements and one incorrect statement.  Put a cross in each row against the incorrect statement.
   

   c Mass is  base quantity	c Charge is a base unit	c Force is a derived quantity
   c Watt=joule/second	c Volt=joule/coulomb	c Coulomb=ampere/second
   c Gradient of displacement/time graph is velocity	c Gradient of velocity/time graph is acceleration	c Gradient of acceleration/time graph is displacement
   c mass is a scalar quantity	c linear momentum is a scalar quantity	c power is a scalar quantity

10.  

Concepts map